Multiplicación de monomios
Producto de un número por un monomio
El producto de un número por un monomio es otro monomio semejante cuyo coeficiente es el producto del coeficiente de monomio por el número.
5 · (2x2 y3 z) = 10x2 y3 z
Multiplicación de monomios
axn · bxm = (a · b)xn +m
(5x2 y3 z) · (2 y2 z2) = 10 x2 y5 z3
1. Suma de monomios
Sólo podemos sumar monomios semejantes.
La suma de los monomios es otro monomio que tiene la misma parte literal y cuyo coeficiente es la suma de los coeficientes.
axn + bxn= (a + b)xn
Ejemplo:
2x2y3z + 3x2y3z =
(2 + 3)x2y3z =
5x2y3z
Si los monomios no son semejantes, al sumarlos, se obtiene un polinomio.
2. Producto de un número por un monomio
El producto de un número por un monomio es otro monomio
semejante cuyo coeficiente es el producto del coeficiente del monomio
por el número.
Ejemplo:
5 · (2x2y3z) = 10x2y3z
3. Multiplicación de monomios
La multiplicación de monomios es otro monomio que tiene por
coeficiente el producto de los coeficientes y cuya parte literal se
obtiene multiplicando las potencias que tengan la misma base.
axn · bxm = (a · b)xn + m
Ejemplo:
(5x2y3z) · (2y2z2) = (2 · 5) x2y3+2z1+2 = 10x2y5z3
4. División de monomios
Sólo se pueden dividir monomios cuando:
1Tienen la misma parte literal
2El grado del dividendo es mayor o igual que el del divisor
La división de monomios es otro monomio que tiene por coeficiente el
cociente de los coeficientes y cuya parte literal se obtiene dividiendo
las potencias que tengan la misma base.
axn : bxm = (a : b)xn − m
Si el grado del divisor es mayor, obtenemos una
fracción algebraica.
5. Potencia de un monomio
Para realizar la potencia de un monomio se eleva, cada elemento de este, al exponente que indique la potencia.
(axn)m = am · xn · m
Ejemplos:
(2x3)3 = 23 · (x3)3= 8x9
(−3x2)3 = (−3)3 · (x2)3= −27x6
Multiplicación de binomios
Los binomios se usan ampliamente en el campo
del álgebra, al igual que en las ciencias físicas y químicas. Los
binomios son expresiones algebráicas que contienen dos monomios y
también se consideran polinomios muy básicos. Los monomios son
expresiones que pueden contener uno o más de los siguientes elementos:
una base, una variable (indicada por una letra) y un exponente. Aunque
parezca complejo, multiplicar dos binomios entre sí es bastante sencillo si estás familiarizado con un par de reglas.
EJEMPLO:
(a + b) . (x + y) =
= a . (x + y) + b . (x + y )
= ax + ay + bx + by
–
(a + b) . (a – b) =
= a . (a – b) + b . (a – b)
= aa – ab + ba – bb
= a
2 -
ab +
ab – b
2
= a
2 – b
2
EJEMPLO Nº 2
- Multiplica el primer término del primer binomio por el primer término del segundo binomio, pero recuerda multiplicar los valores de las bases y sumar los exponentes. Por ejemplo en la expresión (2a + 3b)(a + 7b) debes multiplicar 2a * 1a para obtener 2a^2.
- Multiplica el primer término del primer binomio por el segundo término del segundo binomio (los números "exteriores"). En el ejemplo (2a + 3b)(a + 7b) debes multiplicar 2a * 7b. Este término simplificado equivale a 14ab.
- Multiplica el segundo término del primer binomio por el primer término del segundo (los números "internos"). En el ejemplo (2a + 3b)(a + 7b) debes multiplicar 3b * 1a. Este término simplificado es equvalente a 3ba, o 3ab.
- Multiplica el segundo término del primer binomio por el segundo término del segundo binomio (los "últimos" números). Para el ejemplo (2a + 3b)(a + 7b) debes multiplicar 3b * 7b, que equivale a 21b^2.
- Coloca los cuatro valores en una sola
ecuación, sumándolos entre sí. En el ejemplo (2a + 3b)(a + 7b), tienes
los términos 2a^2, 14ab, 3ab, y 21b^2. Como 14ab y 3ab tienen las mismas
letras, estos pueden sumarse entre sí para simplificar. Por lo tanto la
respuesta del ejemplo es 2a^2 + 17ab + 21b^2.
2 términos × 1 término (binomio por monomio)
Multiplica cada uno de los dos términos por el que está solo, así:
(Hice este un poco más rápido porque multipliqué de cabeza antes de escribir)
2 términos × 2 términos (binomio por binomio)
| Cada uno de los dos términos en el primer binomio |
| se multiplica por |
| Cada uno de los dos términos del segundo binomio |
Eso son cuatro multiplicaciones diferentes... ¿por qué?
 |
Haciendo parejas
Dos amigas (Alicia y Bea) retan a dos amigos (Carlos y David) a partidos individuales de tenis.
|
¿Cuántos partidos son?
- Alicia juega contra Carlos, y después contra David.
- Bea también juega contra Carlos y contra David.
Podrían jugar en cualquier orden, siempre que cada una de las amigas juegue contra cada uno de los amigos. |
¡Es lo mismo cuando multiplicamos binomios!
En lugar de Alicia y Bea, usamos a y b, y Carlos y David pueden ser c y d:
Puedes multiplicarlos en cualquier orden siempre que cada uno de los dos primeros términos se multiplique por cada uno de los dos segundos términos.
Aquí tienes una manera de acordarte de todas las multiplicaciones. "PIES" significa "Primeros, Interiores, Exteriores, Segundos":
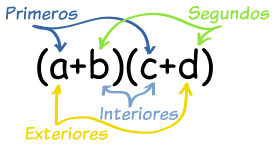 |
- Primeros: ac
- Interiores: bc
- Exteriores: ad
- Segundos: bd
|
Así que multiplicas los "Primeros" (el primer término de cada polinomio), después los "Interiores", etc.
Multiplicación de Polinomios
1. Multiplicación de un número por un polinomio
Es otro polinomio que tiene de grado el mismo del polinomio y
como coeficientes el producto de los coeficientes del polinomio por el
número y dejando las mismas partes literales.
Ejemplo:
3 · (2x3 − 3x2 + 4x − 2) = 6x3 − 9x2 + 12x − 6
2. Multiplicación de un monomio por un polinomio
Se multiplica el monomio por todos y cada uno de los monomios que forman el polinomio.
Ejemplo:
3x2 · (2x3 − 3x2 + 4x − 2) =
= 6x5− 9x4 + 12x3 − 6x2
3. Multiplicación de polinomios
Este tipo de operaciones se puede llevar a cabo de dos formas distitnas.
Mira la demostración con el siguiente ejemplo:
P(x) = 2x2 − 3
Q(x) = 2x3 − 3x2 + 4x
OPCIÓN 1
1Se multiplica cada monomio del primer polinomio por todos los elementos del segundo polinomio.
P(x) · Q(x) = (2x2 − 3) · (2x3 − 3x2 + 4x) =
= 4x5 − 6x4 + 8x3 − 6x3+ 9x2 − 12x =
2Se suman los monomios del mismo grado.
= 4x5 − 6x4 + 2x3 + 9x2 − 12x
3Se obtiene otro polinomio cuyo grado es la suma de los grados de los polinomios que se multiplican.
Grado del polinomio = Grado de P(x) + Grado de Q(x) = 2 + 3 = 5
OPCIÓN 2





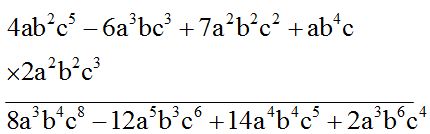
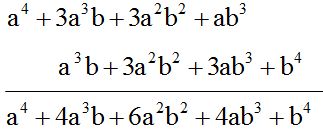
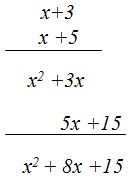
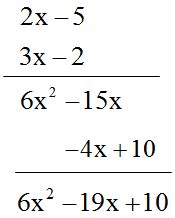
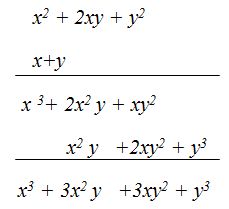
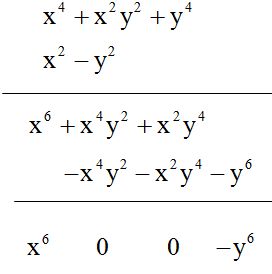
 RESPUESTA
RESPUESTA




















