QUE SON LAS PROPOSICIONES LOGICAS

es una oración que puede ser falsa o verdadera pero ambas a la vez . son elementos fundamentales de la logia matematicas.
ejemplo:
p: x>y-9=   proposición

se clasifican en dos que son
SIMPLES Y COMPUESTAS

simples: no tienen oración afectada por los terminos de negación
conjunción      (y)
disyunción       (o)
negación           (no)
implicación       (si)  entonces

compuesta: si esta afectada por los teminos

qué es un enunciado?
en el conjuto de palabras con las que se expone o plantea.



PROPOSICIONES

llamamos de esta forma  a cualquier afirmación que sea verdadera o falsa , pero no ambos a la vez.
ejemplo:

Grabriel Garcia Masquez escribio cien años de soledad.
6 es un número primo
1 es un númetro entero, pero 2 no lo es.

Variable

Para una variable lógica A, B, C, ... que pueden ser verdaderas V, o falsas F, los operadores fundamentales se definen así:

Negación

La negación es un operador que se ejecuta, sobre un único valor de verdad, devolviendo el valor contradictorio de la proposición considerada.

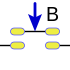
Conjunción

La conjunción es un operador que opera sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones son verdaderas, y falso en cualquier otro caso. Es decir es verdadera cuando ambas son verdaderas
La tabla de verdad de la conjunción es la siguiente:

Que se corresponde con la columna 8 del algoritmo fundamental.

Disyunción

La disyunción es un operador que opera sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando una de las proposiciones es verdadera, o cuando ambas lo son, y falso cuando ambas son falsas.
La tabla de verdad de la disyunción es la siguiente:

Implicación o Condicional

El condicional material es un operador que opera sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de falso sólo cuando la primera proposición es verdadera y la segunda falsa, y verdadero en cualquier otro caso.
La tabla de verdad del condicional material es la siguiente:

Que se corresponde con la columna 5 del algoritmo fundamental.

Equivalencia o Bicondicional

El bicondicional o doble implicación es un operador que funciona sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones tienen el mismo valor de verdad, y falso cuando sus valores de verdad diferente.
La tabla de verdad del bicondicional es la siguiente:

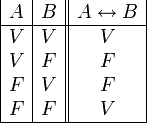
 unidad n°2
sistema de numeración
es un conjunto de simbolos para repesentar cantidades
(0123456789)10sistema decimal
(012345678)9  sistema nonario


Los sistemas de numeración pueden clasificarse en dos grandes grupos: posicionales y no-posicionales:

• En los sistemas no-posicionales los dígitos tienen el valor del símbolo utilizado, que no depende de la posición (columna) que ocupan en el número.
• En los sistemas de numeración ponderados o posicionales el valor de un dígito depende tanto del símbolo utilizado, como de la posición que ése símbolo ocupa en el número.

Por ejemplo, el sistema de numeración egipcio es no posicional, en cambio el babilónico es posicional. Las lenguas naturales poseen sistemas de numeración posicionales basados en base 10 ó 20, a veces con subsistemas de cinco elementos. Además, en algunas pocas lenguas los numerales básicos a partir de cuatro tienen nombres basados en numerales más pequeños

 decimal a binario




NÚMERO DECIMAL 8 TRANSFORMADO AL SISTEMA BINARIO

SISTEMA DECIMAL

valor absoluto: En el sistema decimal, con base, o raíz, igual a 10,

Cuando el número se hace igual a la raiz -en este caso 10- , ya no lo podemos representar mediante un dígito, sino que tenemos que recurrir a otro digito más.

valor relativo: El valor de asignación que toma cada dígito depende de su posición respecto al punto decimal. Este valor asignado siempre es potencia de diez.

EJEMPLO:

Así, en el sistema decimal en número decimal 567 se desglosaría:

número decimal: 567
5 x (102)	5 x 100	= 500
6 x (101)	6 x 10	= 60
7 x (100)	7 x 1	= 7
	Total (nº decimal)	567

Conversión de decimal a binario

Para convertir números enteros de decimal a binario, la forma más simple es dividir sucesivamente el número decimal y los coeficientes que se van obteniendo por 2, hasta que el cociente en una de las divisiones se haga 0.

La unión de todos los restos obtenidos escritos en orden inverso nos proporciona el número inicial expresado en el sistema binario.

EJEMPLO:

Conversión (sistema decimal) a sistema binario
15	2
1	7	2
	1	3	2
		1	1

1510= 11112, (o, lo que es lo mismo: la cifra quince en base diez es igual a la cifra 1111 en base dos)

SISTEMA BINARIO

valor absoluto: En el sistema binario, de base 2, la posición de cada dígito binario respecto al punto binario, determina su valor asignado..

Cuando el número se hace igual a la raiz -en este caso 2-, ya no lo podemos representar mediante un dígito, sino que tenemos que recurrir a otro digito más.

valor relativo: El valor asignado en este caso será una potencia de 2, y no una potencia de 10 como en el sistema decimal.

Así, podemos transformar el número binario 1011, en su equivalente decimal:

EJEMPLO:

número binario: 1011
1 x 23	= 1 x 8	= 8
0 x 22	=0 x 4	=0
1 x 21	=1 x 2	=2
1 x 20	=1 x 1	=1
Total (nº decimal)		11

10112=1110

(o, lo que es lo mismo: la cifra 1011 en base dos es igual a la cifra 11 en base diez)

SISTEMA EXADECIMAL

valor absoluto: En el sistema de numeración hexadecimal, que utiliza la base 16 para representar los números que van del 10 al 15 mediante las letras que van de la A a la F.

• Los números del 0 al 9: 0,1,2,3,4,5,6,7,8,9 y
• Las letras A, B, C, D, E, F (A=10, B=11, C=12, D=13; E=14: F=15.)

EJEMPLO:

número hexadecimal: 2CA
2 x 162	= 2 x 162 (256)	=512
C x 161	= 12 x 161 (16)	=192
A x 160	= 10 x 160 (1)	=10
Total (nº decimal)		714

2CA16=71410 (o, lo que es lo mismo: la cifra 2CA en base dieciseis es igual a la cifra 714 en base diez)

TABLAS DE EQUIVALENCIAS


                                                    
                                                       TABLA DE EQUIVALENCIA

BLAS EQUIVALENCIA ENTRE LOS DIFERENTES SISTEMAS
DECIMAL	BINARIO	OCTAL	HEXADECIMAL					DECIMAL	BINARIO	OCTAL	HEXADECIMAL
0	0	0	0					9	1001	11	9
1	1	1	1					10	1010	12	A
2	10	2	2					11	1011	13	B
3	11	3	3					12	1100	14	C
4	100	4	4					13	1101	15	D
5	101	5	5					14	1110	16	E
6	110	6	6					15	1111	17	F
7	111	7	7					16	10000	20	10
8	1000	10	8					17	10001	21	11

I