Multiplicación de monomios
Producto de un número por un monomio
El producto de un número por un monomio es otro monomio semejante cuyo coeficiente es el producto del coeficiente de monomio por el número.
ejemplo:
5 · (2x2 y3 z) = 10x2 y3 z
Multiplicación de monomios y polinomios.
Objetivo:
Para llevar a cabo la
multiplicación algebraica se deben aplicar 3 pasos.
1. Se lleva a cabo la
multiplicación de los signos, debes recordar que:
( + ) ( + ) = +
( - ) ( - ) = +
( - ) ( + ) = -
( + ) ( - ) = -
2. Multiplicar los coeficientes.
3. Se efectúa la
multiplicación de literales; aquí se presentan casos:
a)
Cuando se tienen las mismas literales.
En este caso se tiene que
poner a cada una de las literales un exponente igual a la suma de los exponentes de las
letras iguales, ejemplo;
a2 . a3 . a6 = a 2+3+6 =
a"
x2 y z3 . x y3 z2 = x2+1=3
. y1+3=4. z3+2=5
= x3 y4 z5
b) Cuando los factores tienen literales
diferentes; entonces se escriben las literales ordenándolas alfabéticamente. a,b,c,z...
a . b. z= abz
x2y . a . c2 d2= ac2 d2
x2 y
Ejemplos
1. (5x) (-4x2) = - 20 x3
2. (-3x2y)(xy2)(- 7ay) = + 21 ax3
y4
3. (3 x y)(- ab )(-5ab x3y2) = 15 a2
b2 x4 y3
Ejercicios:
Realiza las siguientes
operaciones:
1. (-3xy)2 (5y2) (2x2 y3)
2. (2x3 y1/2z) (-4x y 3/2x2)
3. ( 8x-2)(9 x3 y4) (-5xy)
4. (-3xy) [ -(-2x3y)(6x)]
5. (7a3) (-2ab) (-3ab1/2)
Solución:
1. 90x4y7
2. -8x6y2 z
3. 360 x2 y5
4. 36 x5 y2
5. 42 a5 b3/2
ejercicios resueltos
1. (a + 2)(a + 3) = a² + a (2 + 3)+(2)(3)
= a² + 5a + 6
2. (x + 5)(x + 4) = (x)² – x (5 + 4) + (5)(4)
= x² + 9x + 20
3. (t + 2)(t - 3) = t² + t (2 – 3) + (2)(-3)
= t² - t - 6
(a + 5)(a - 9) = a² + a (5 – 9) + (5)(-9)
= a² – 4a – 45
5. (x - 8)(x - 1) = (x)² + x(- 8 + -1) + (- 8)(- 1)
= x² - 9x + 8
6. (a - 7)( a – 9) = (a)² + a (-7 + -9) + (-7)(-9)
= a² - 16 a + 63
7. (x + 2)(x - 12) = (x)² + x(2 - 12) + (2)(-12)
= x² – 10x - 24
8. (x + 3)(x + 8) = x² + x(3 + 8) + (3)(8)
= x² + 11x + 24
9. (x – 4)(x - 6) = (x)² + x(- 4 + - 6) + (-4)(- 6)
= x² - 10x + 24
10. (x + 6)(x - 2) = (x)² + x(6 – 2) + (6)(-2)
= x² + 4x - 12
11. (x – 3)(x - 8) = (x)² + x(-3 + - 8) + (- 3) (- 8)
= x² - 11x + 24
12. (x – 13)(x + 2) = (x)² + x (-13 + 2) + (-13)(2)
= x² - 11x - 26
13.- (a – 7)(a + 12)= (a)² + a(-7)(12) +(- 7+ 12)
= a² + 5a - 84
14. (x² + 5)(x² + 3) = (x²)² + x²(5 + 3) + (5)(3)
= x⁴ + 8x² + 15
15. (a ² – 3)(a² + 4) = (a²) ² + a² (-3 + 4) + (- 3)(4)
= a⁴ + a² - 12

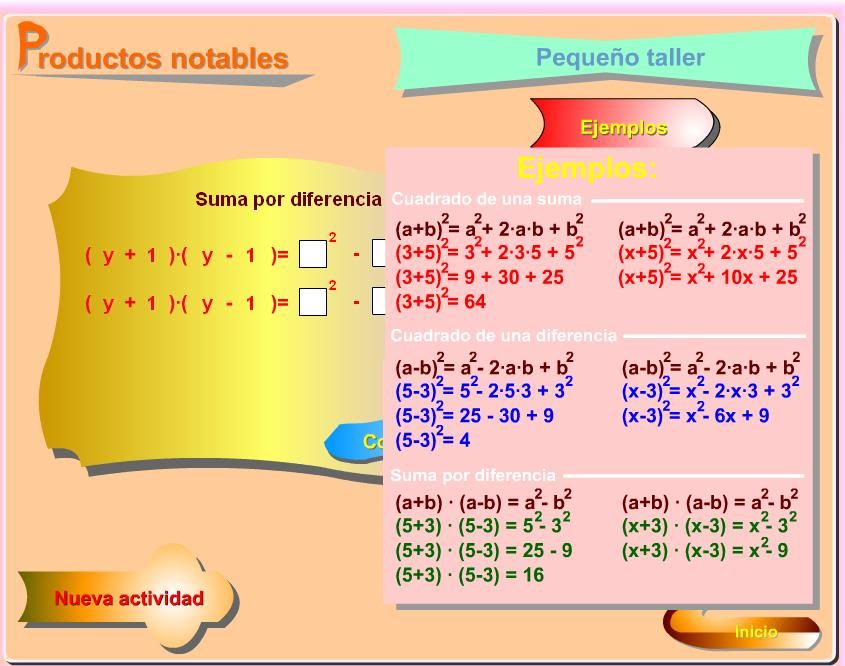



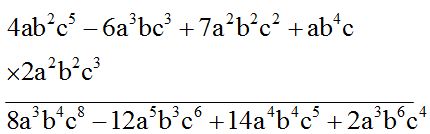
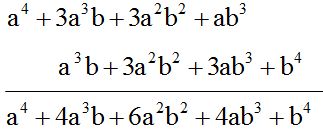
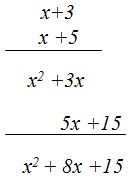
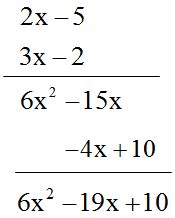
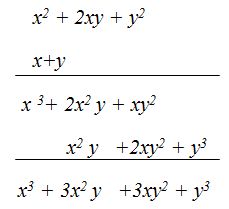
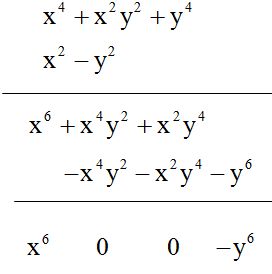
 RESPUESTA
RESPUESTA